量化研究 | 终极平滑器

量化策略开发,高质量社群,交易思路分享等相关内容
终极平滑器
通过减少滞后平滑数据
首先,我们向您介绍了一种超级平滑器。这里,我们介绍一种终极平滑器。这是一个您不容错过的进步。
平滑器是一种低通滤波器,它通过输入数据频谱的低频成分而几乎不改变,并拒绝或衰减数据中的高频成分。通过抑制高频成分,产生的输出波形比输入波形更平滑。在我的工程职业生涯初期,我使用线圈电感器和实际电容器设计滤波器。这种经验使我能够发明超级平滑器以及终极平滑器,我将在本文中描述后者。
SuperSmoother(超级平滑器)
超级平滑器数字滤波器是从一种模拟滤波器翻译而来,该模拟滤波器具有最大平滑度但具有较低衰减的低通滤波器响应。超级平滑器的代码如旁栏所示,标题为“简易语言中的超级平滑器函数”。这里,它被编写为一个函数,因此可以像移动平均线一样轻松地用于指标和策略中。
超级平滑器是一种二阶无限冲激响应(IIR)滤波器,这意味着它使用了滤波器输出的两个先前计算结果进行当前滤波响应的计算。超级平滑器的定义参数是临界周期。临界周期是划分通带和阻带的波长。从概念上讲,可以将其视为通带所有较长波长通过而输出且所有较短波长在输出处被完全拒绝的波长。实际上,从通带到阻带的过渡是逐渐变化的。过渡的锐度在很大程度上取决于IIR滤波器的阶数。为了简洁,临界周期是代码列表中“超级平滑器函数”旁栏中的“周期”。
指数移动平均线(EMA)是一阶IIR滤波器,仅使用一个先前的计算。它是由以下公式描述的平滑器:
EMA = alpha * 价格 + (1 - alpha) * EMA[1]
其中EMA[1]是前一个K线的EMA值。
可以通过将alpha设置为3除以周期来比较EMA的性能和超级平滑器的性能。旁栏中的代码用于绘制这两种平滑器的比较,如图1所示。
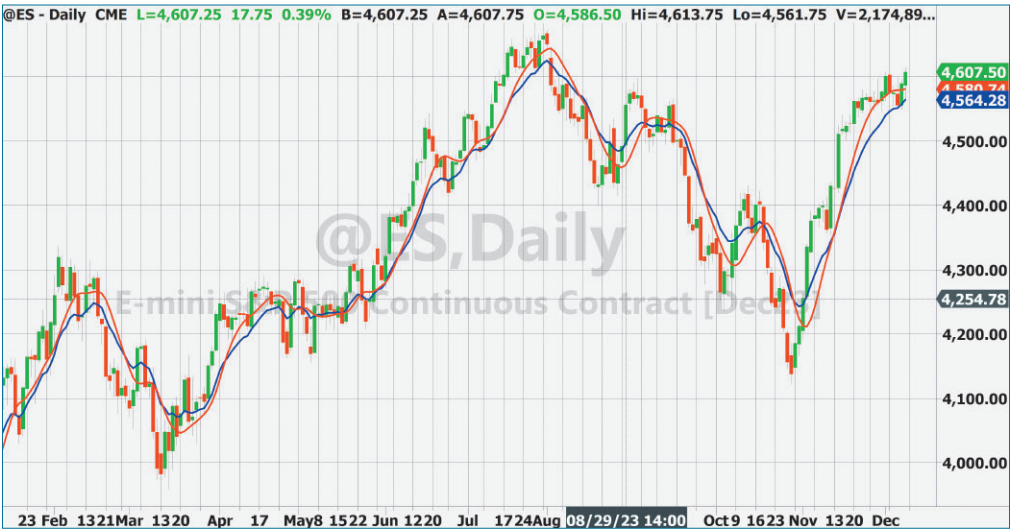
图1:超级平滑器:对于同样的滞后,超级平滑器的响应比EMA更好。
显然,二阶超级平滑器(红色)比具有相同临界周期的一阶EMA(蓝色)表现出更好的平滑效果。显而易见的是,两种滤波器对输入数据的滞后都很大。滞后是交易者的一个主要问题。它没有帮助,如果在最后时刻得不到正确答案。
可以设计更高阶的平滑器。更高阶的滤波器使通带到阻带的过渡更加锐利。然而,代价是这些滤波器的滞后更大。因此,这些更高阶的滤波器很少用于交易。此外,更高阶滤波器的计算会导致许多交易平台上的浮点错误。第四阶滤波器的合理近似是首先用超级平滑器过滤数据,然后再用超级平滑器过滤结果。
(High-pass)高通滤波器
低通滤波器并不是唯一可以使用的滤波器。可以通过将传递函数中的零点替换为零频率处的零点来创建二阶高通滤波器。在 Nyquist 频率处的响应(样本周期的两倍)具有零频率的零点。这意味着,输入数据的低频成分在滤波器输出处被拒绝,而高频成分几乎不衰减地通过输出。
(band-pass)带通滤波器
(在信号处理和电子工程中,“带通”通常指一种滤波器或电路,它允许特定频率范围内的信号通过,而阻止其他频率的信号。带通滤波器用于从信号中提取或传输特定频段的频率,常见于音频处理、无线电通信和其他领域。)
另一种可以设计的滤波器是带通滤波器。使用这种类型的滤波器,存在一组几乎不衰减地传递到输出的周期,长于较低临界周期的周期被拒绝,高于上临界周期的周期也被拒绝。我已经设计了几种二阶带通滤波器,但我不建议使用它们,因为有可能使用这种滤波器产生看起来类似于正弦波的输出。正弦波的出现是由于滤波器仅通过一个相对较窄的带宽,该带宽从数据频谱的通带到输出。当带宽在中心周期的25%或更少时,相位响应几乎是连续的。使用这种滤波器可以在输出中获得惊人的相位响应。但如果数据频谱稍有不同,输出波形可能会由于180度相位反转而给出错误的交易信号。识别输入数据中的这种变化几乎在实时中是不可能的。

要创建一个更好的带通滤波器响应,可以按照以下步骤进行:
1. 使用一个超级平滑器滤波器,将其周期设置为通带的最高频率对应的周期。
2. 使用一个高通滤波器,将其周期设置为通带的最低频率对应的周期。
确保最低频率和最高频率之间的间隔至少是一个八度(即频率加倍)。这样,可以使整个通带内的相位变化保持相对一致。

提供了一个带通滤波器的例子。通带设置为15个条周期和30个条周期之间的一个八度(频率加倍)。这个设置可以根据数据集调整,以获得最佳结果。图2显示了这种带通滤波器响应的例子。带通滤波器的输出是一个振荡器风格的指标,可以直接作为指标使用。图2展示了该滤波器响应的例子。
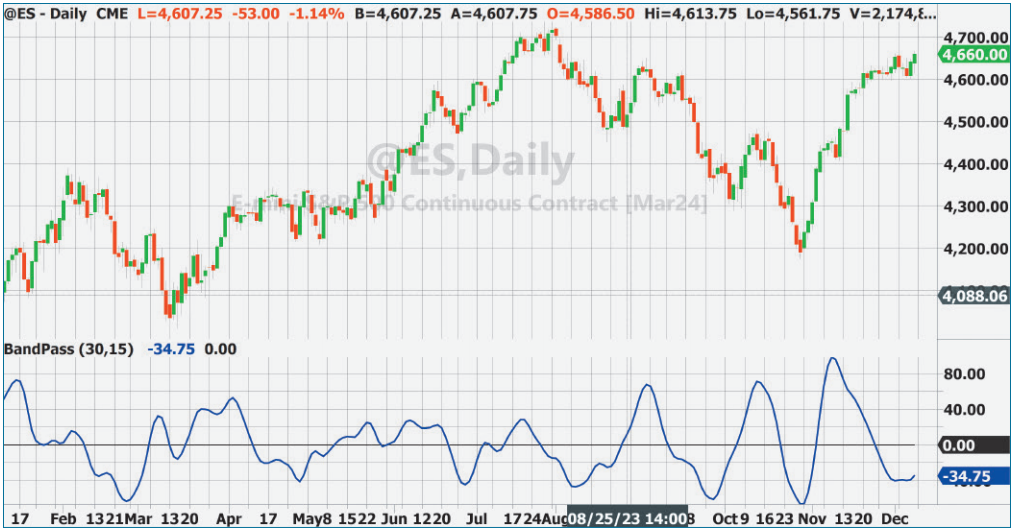
图2:带通滤波器。带通滤光器输出振荡器式指示器输出。
这个带通滤波器优于二阶带通滤波器,因为它在通带和阻带之间提供了更锐利的过渡。可以这样理解:二阶带通滤波器在上滤波器边缘应用一阶,在下滤波器边缘应用一阶,而这个带通滤波器在上下滤波器边缘都应用了两阶。
像带通滤波器一样,终极平滑器由两个组件滤波器组成。平滑滤波器的输出通常会有延迟,尽量避免这种情况。根据我的模拟滤波器设计经验,我知道低频滤波器需要更大的电感和电容,这种滞后是由于需要积聚电场和磁场能量所致。想想用于低频声音的大低音扬声器和产生高频声音的小高音扬声器。这种概念在数字滤波器中消失了,但原理是一样的。你知道移动平均线变得越长,滞后越大。这与向滤波器中添加更多能量是一样的。你还知道,较长的移动平均线有更多的滞后。
终极平滑器在通带中概念上没有滞后,并且在过渡带中的滞后最小,因为只涉及一个高频滤波器。终极平滑器的原理如图所示。

图3中的示意图中,输入数据在数学上描述为全通滤波器,以黑色显示。终极平滑器响应是通过从全通滤波器响应中减去高通滤波器响应获得的,如红色所示。在非常低的频率下,高通滤波器几乎没有幅度,所以减法的结果是终极平滑器输出与输入数据在幅度和滞后方面基本相同。另一方面,高通滤波器的响应几乎与输入数据相同,因此通过抵消来完成滤波。
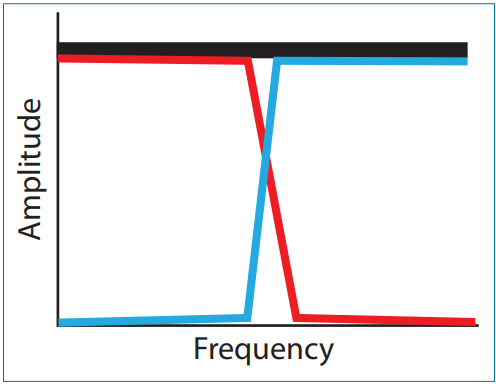
图3:终极平滑器的导出。终极平滑器通过从输入数据(黑色)中减去高通滤波器响应(蓝色)来构建。结果滤波器响应以红色显示。
对于数学上倾向的,减去高通滤波器的全通滤波器传递函数描述为:
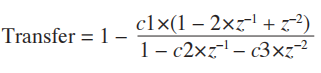
把分母统一,传递函数以闭合形式为:
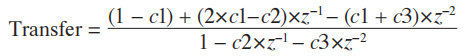

终极平滑器的示例绘制在图4中。终极平滑器的一个惊人特点是它在通带中没有滞后。图4中缺乏滞后可以与图1中超级平滑器和EMA的滞后进行比较。在所有情况下,临界周期都设置为20个条。终极平滑器可以应用于任何输入数据,包括其他指标。
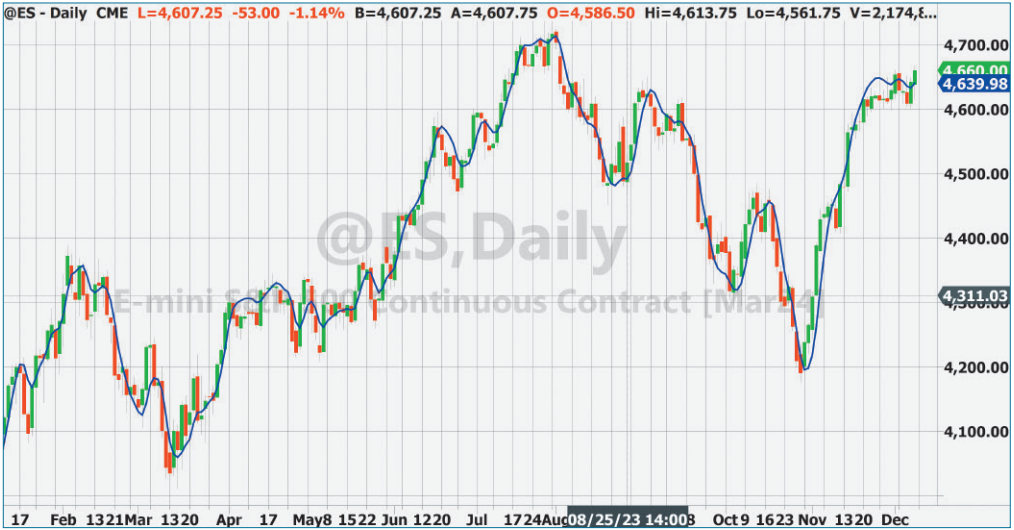
图4终极平滑器。终极平滑器在通带的滞后为0
结论
1. 终极平滑器在通带中没有滞后。
2. 终极平滑器通过从输入数据中减去高通滤波器的响应来创建。
3. 终极平滑器的输出不像超级平滑器那么平滑,因为滤波是通过抵消完成的。高通滤波器在其通带中的幅度和相位响应与输入数据不完全相同。
4. 推荐使用超级平滑器代替EMA。在大多数情况下,它还可以代替简单的移动平均线。
5. 最好的带通滤波器是通过串联高通滤波器和超级平滑器来创建的。
6. 带通滤波器的带宽应超过一个八度。
7. 终极平滑器, 超级平滑器和高通滤波器的代码提供为函数,可以像移动平均线一样轻松调用。
8. 临界周期是滤波器的定义参数。临界周期描述了将通带与阻带分开的周期。
代码
源码已经上传至俱乐部,小助理:viquant01 加入2024俱乐部
