量化研究 | 利用均线过滤震荡的多种算法(源码)

量化策略开发,高质量社群,交易思路分享等
工具推荐
可直接跳到:量 化 说 人话
在统计学和信号处理中,当波形或数据序列与窗口函数相乘时,结果就是它们重叠的部分,通常被认为是“透过窗口看到的景象”。窗口函数可以改善用于交易的滤波器的功能,例如简单移动平均线。哪种窗口函数最适合用于此?我们将一探究竟。
简单移动平均线(SMA)在技术分析中无处不在。然而,事实是它们并不是很好的滤波器。本文的目的是介绍一些简单、易于编程的修改,这些修改代表了在技术分析中使用时,在滤波和滞后之间近乎最佳的折衷方案。
一组数据点的真实值的最佳统计估计是这些数据点的平均值。在时间序列的情况下,用于平均的数据点组可以选择为一个分析长度。然后,这个组通过丢弃最旧的数据点并添加新的数据点来改变。这就是移动平均线。从这个意义上说,简单移动平均线通过连接这些点来创建时间序列的最佳估计。然而,每个滤波器输出的时间中心是每个平均值的水平中心。因此,群延迟滞后大约是平均周期长度的一半。这种滞后是不可避免的,无法在移动平均线类型的滤波器中改变。
一些交易者试图通过将滤波结果中心化到当前柱线后半部分来抵消SMA的滞后。然而,这并不奏效,因为交易是在图表的最右边缘进行的,而中心化的移动平均线在那里并不存在。因此,中心化的移动平均线应予避免。修补缺失数据的方法根本行不通。
简单移动平均线可以被视为在平均周期内将数据点乘以1,而将所有其他数据点乘以0。因此,乘数因子的轮廓是一个矩形窗口,其系数均为1。随着平均的进行,窗口只是沿着数据流滑动。
时域中的乘法是频域中的卷积。这意味着简单移动平均线的频率响应是矩形窗口的傅里叶变换。矩形窗口的傅里叶变换是教科书上的内容,其形状为sine(X)/X,其中X = πfL,L是矩形窗口的长度(以数据样本为单位),f是归一化频率,范围从最小的0到最大的奈奎斯特频率0.5。
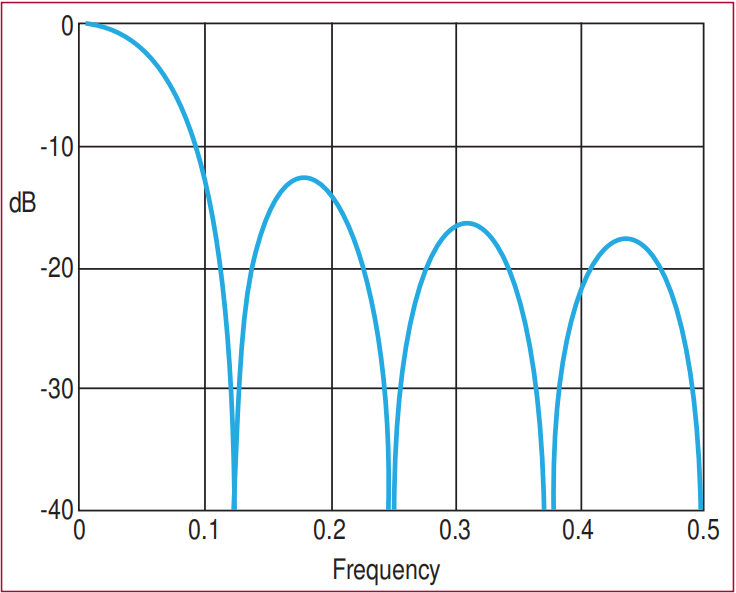
图1:显示了一个八元素简单移动平均线的频率响应。交易者更喜欢用波长而不是频率来思考。波长是频率的倒数。因此,奈奎斯特频率0.5对应两根柱线的波长,频率0.1对应十根柱线的波长,等等。
参考图1,SMA是一个低通滤波器,这意味着它通过非常低的频率并衰减较高的频率。SMA的频率响应在数据波长是窗口长度的倍数时会出现零点,因为傅里叶变换的分子在正弦函数的参数是π的倍数时会变为零。第一个零点出现在频率0.125(波长8)。滤波器的通带被定义为滤波器将数据衰减到其功率一半的频率,即-3 dB点。这发生在频率0.056。更容易记住的近似值是-3 dB点出现在第一个零点波长的一半处。也就是说,SMA的半功率点出现在波长是SMA窗口长度两倍的频率处。在图1的情况下,这个频率是0.0625。
SMA滤波器的第一旁瓣峰值大约出现在sine(X)/X函数的分子为1时。在这种情况下,频率是1/(1.5L),X=1.5π。如果分子为1,那么滤波器传输响应的值就是X的倒数,即-13.5 dB。这并不是很大的衰减。在这个频率下,数据的幅度仅减少到其未过滤值的大约21%。这种较差的衰减通常被称为滤波器的“旁瓣泄漏”。作为参考,与其他滤波器相比,SMA的频率响应在频率0.092处穿过可识别的-10 dB网格线。
顺便说一句,作为一名学生,我曾困惑于为什么sine(X)/X在X趋近于零时渐近地趋近于1。有理函数通常在分母趋近于零时发散。答案是通过考虑正弦函数的幂级数展开得到的。它是:正弦(X) = X - X³/3! + X⁵/5! - ........ 因此,如果X非常小,那么除了第一项外,所有其他项都可以忽略不计。因此,当X趋近于零时,sine(X)/X趋近于1。我想小事情也能让伟大的头脑感到愉悦。
我希望将加权移动平均线类型的滤波器排除在这次讨论之外。加权移动平均线被提议作为一种减少滞后的方法。然而,它们具有指数移动平均线中发现的所有相位失真的不良特性,并且还具有简单移动平均线中作为滤波器长度函数的群延迟滞后特性。它们兼具了所有最糟糕的特性。因此,我将只讨论有限脉冲响应(FIR)滤波器,其系数关于滤波器中心点对称。
脉冲是一个数学矩形,具有无限高度和零宽度,使得矩形的面积为1。更非正式地说,可以将其视为数据尖峰。FIR滤波器是一种当脉冲在滤波器有限窗口长度内时滤波器有输出的滤波器。SMA是FIR滤波器的一个特例,其窗口形状为矩形。但FIR滤波器的系数可以描绘出任何轮廓形状,只要窗口关于其中心点对称即可。SMA之所以具有如此差的频率响应,是因为矩形窗口形状在前缘和后缘处急剧不连续。当在开始和结束处出现平滑过渡时,会获得更好的滤波效果。好的滤波器系数轮廓会更像钟形曲线而不是矩形。
有数以亿计的窗口函数(维基百科,“窗口函数”)。大多数难以编程。许多具有如此缓慢的过渡,以至于大量数据样本对滤波的贡献最小。这意味着滤波器必须非常长才能接近从SMA获得的相同程度的平滑。这意味着虽然这样的滤波器是很好的滤波器,但它们具有很大的滞后。在交易中,最好得到一个没有滞后的大致答案,而不是在十根柱线后得到正确的答案。
三角形窗口加权 也许最容易编程的窗口具有三角形加权。例如,一个八元素FIR滤波器的系数为[1 2 3 4 4 3 2 1]/20。你希望将每个系数除以总和,以使滤波器在零频率处具有单位增益。这个想法在取平均值时也被使用。
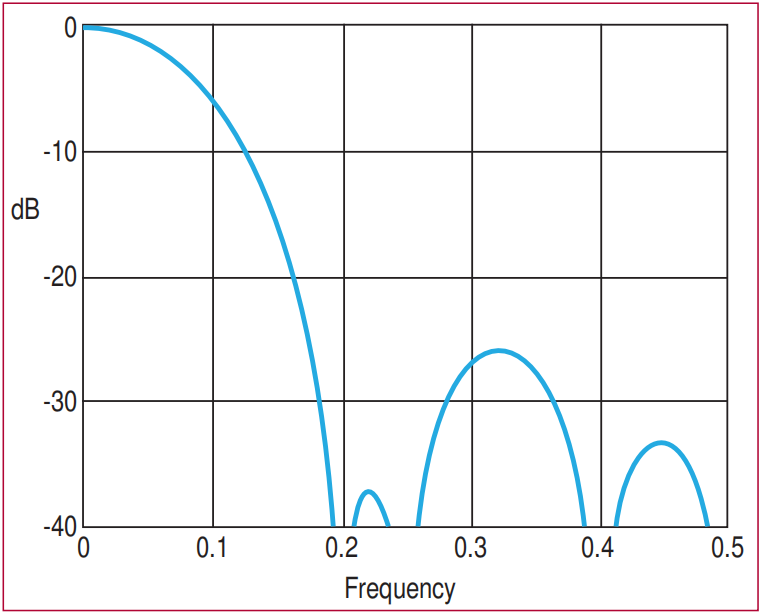
图2:尽管三角形加权仍然存在不连续性,但其频率响应相比SMA有了显著改善。最高的旁瓣在-26 dB,这是一个令人震惊的13 dB改进。半功率带宽增加到0.072,与SMA带宽进行图形比较时,响应在-10 dB水平处的频率为0.125。注意第一个零点的频率也增加了。波束宽度的增加是由于没有充分利用所有系数的全幅度,导致效率降低。SMA半功率波束宽度与窗口滤波器波束宽度的比值称为孔径效率。在这种情况下,三角形加权的孔径效率为77.8%。
Hamming窗口 另一种易于编程的加权称为Hamming窗口。系数形状的轮廓被称为“基座上的余弦”,尽管系数更方便地计算为正弦函数。
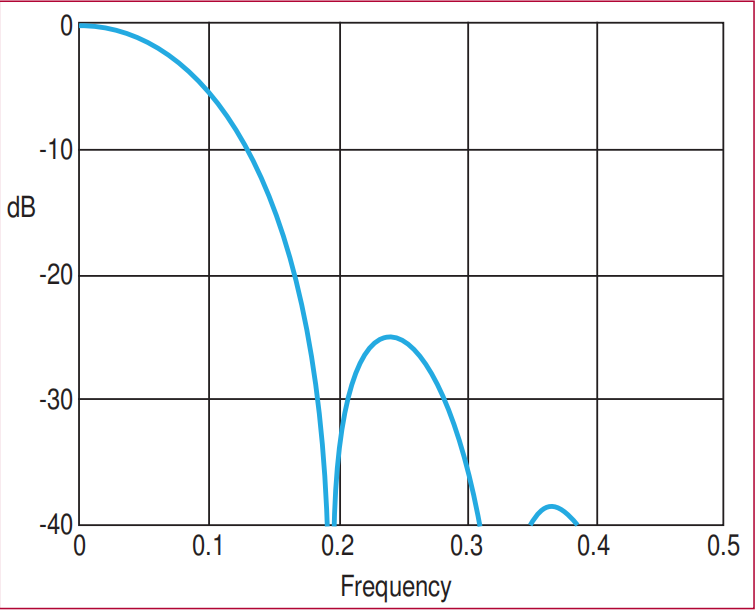
图3:显示了一个八元素Hamming窗口的频率响应,其中第一个元素的基座高度为10度的正弦值。最高的旁瓣在-25 dB,与三角形分布获得的最大旁瓣水平大致相同。然而,由于窗口是一个更平滑的函数,几乎所有的其他旁瓣都低于-40 dB。半功率波束宽度在频率0.074,与三角形分布大致相同。
Hann窗口 一种更平滑且易于编程的加权函数称为Hann窗口。Hann窗口通常被描述为“正弦平方”分布,尽管将其编程为从1中减去余弦更容易。系数轮廓的形状看起来像一个正弦波,其谷值在数组的两端,峰值在数组的中心。这种配置提供了从最小系数幅度到最大系数幅度的平滑窗口过渡。
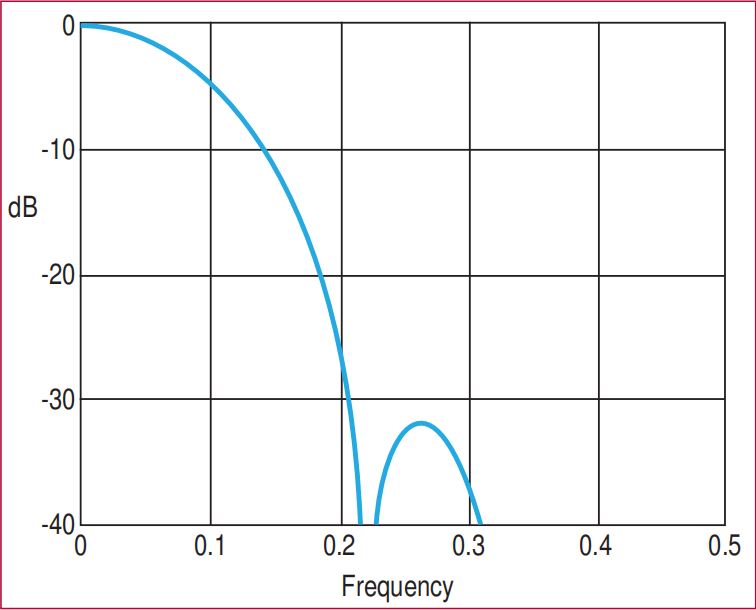
图4:显示了一个八元素Hann窗口的频率响应。最高的旁瓣在-32 dB,这是易于编程的窗口替代方案中最好的。半功率带宽在频率0.08,仅比Hamming窗口产生的半功率带宽略大。
那么,这些窗口函数中哪一种最适合使用?这归结为编程简便性、最小化旁瓣泄漏以及为获得所需平滑度而引入的群延迟滞后之间的权衡。从滤波的角度来看,没有明确的“最佳”答案。
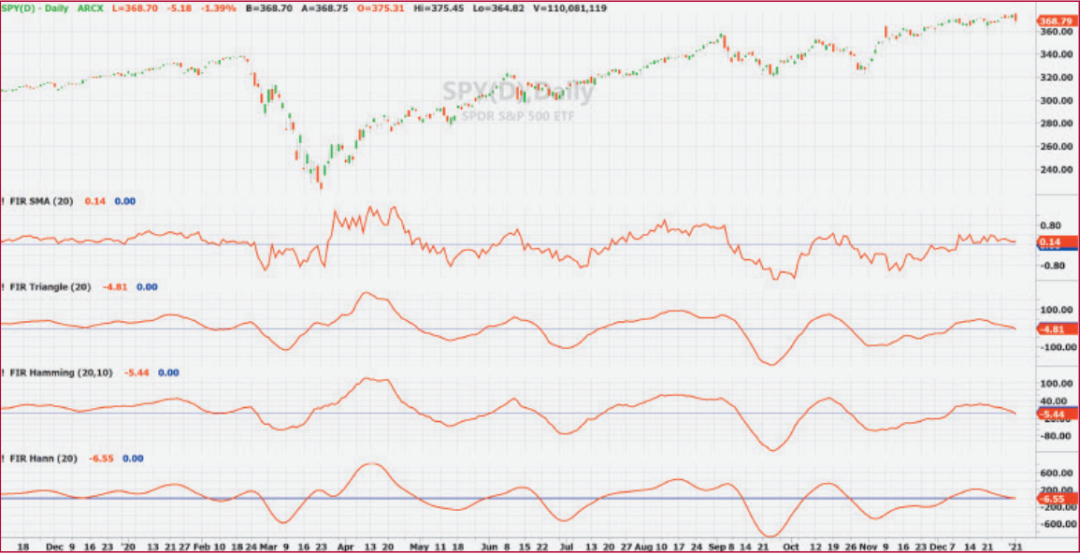
图5:显示了这四种FIR滤波器的对比,它们的长度参数都设置为20。它们看起来大致相同,只是SMA明显比窗口版本更嘈杂。
然而,从交易的角度来看,Hann窗口是明显的赢家。我经常使用滤波器的变化率(ROC)来帮助我的交易决策。ROC识别出滤波数据的峰值和谷值,这些峰值和谷值恰好出现在ROC穿过零点时。因此,拥有相对平滑的ROC对于做出明确的交易决策非常重要。变化率操作本身是一个高通滤波器,因此它会夸大滤波器的高频噪声。
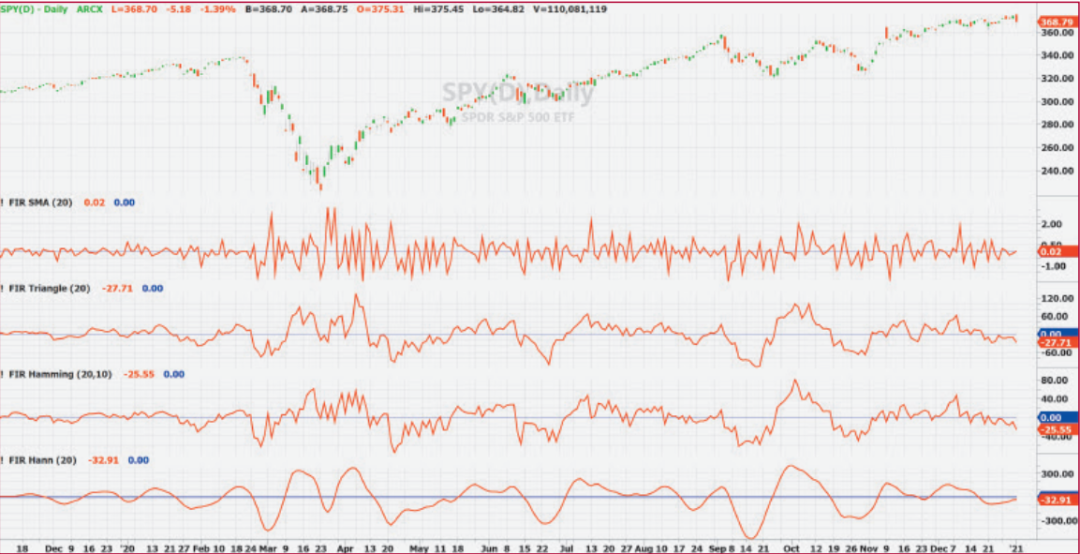
图6:四种窗口化FIR滤波器的ROC平滑性对比。绘制这四个滤波器的ROC(变化率)可以展示它们相对的噪声水平。所有滤波器均设置为20根柱线的长度。SMA的ROC最为嘈杂,而汉宁窗口产生的波形则明显更为平滑。
当你在图6中绘制这四个滤波器的ROC时,可以看到相对的嘈杂程度。所有滤波器都设置为20根柱线的长度。SMA的ROC非常非常嘈杂。三角形窗口的ROC更平滑,甚至比具有10度基座的Hamming窗口的ROC更平滑。通过减小基座尺寸(直到某个限制),可以使Hamming窗口更平滑。但这样做并没有多大好处,因为Hann窗口产生的波形明显更平滑。
总之
窗口函数可以改善简单移动平均线在交易中的功能。选择要使用的窗口函数是在它们的编程简便性之间进行权衡,以及窗口引入的所需平滑度和群延迟滞后之间的权衡。在许多情况下,三角形窗口函数可能已经足够好,因为它超级容易编程。如果使用变化率来帮助做出交易决策,那么使用Hann窗口无疑是最佳选择。
量 化 说 人 话
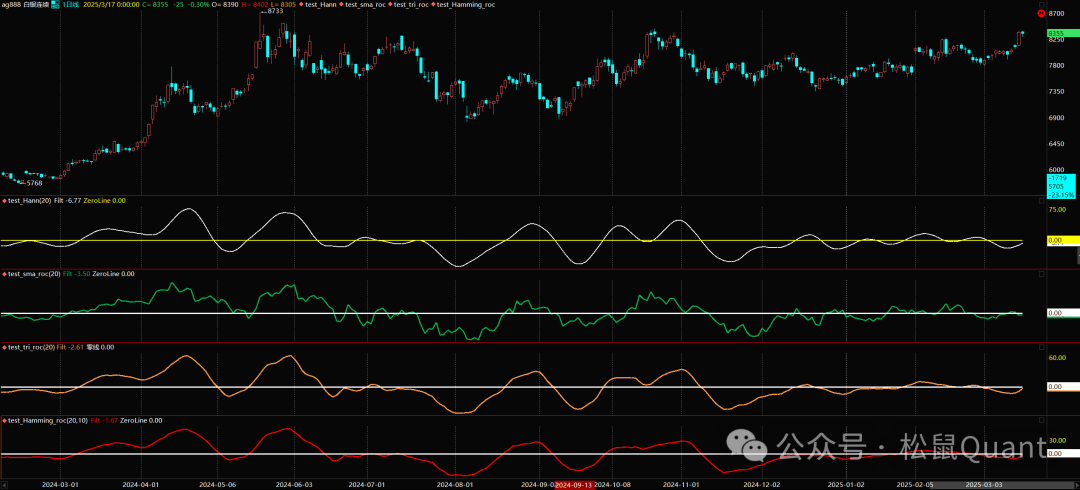
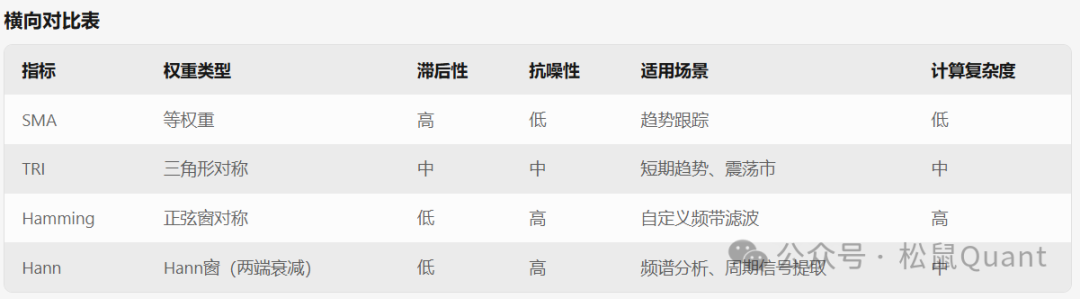
SMA_ROC:平直权重(所有数据权重相同)。 TRI_ROC:三角形权重(中间高,两端低)。 Hamming/Hann_ROC:两端衰减的窗函数。
SMA_ROC:最平滑,滞后最多。 TRI_ROC:响应速度中等,部分保留细节。 Hamming_ROC/Hann_ROC:高频细节保留,滞后最小。
选择建议
趋势跟踪:优先选择 SMA_ROC 或 TRI_ROC(需平衡滞后与灵敏度)。
震荡市滤波:使用 TRI_ROC 或 Hamming_ROC(自定义Pedestal)。
频谱分析:必须使用修正后的 Hann_ROC。
实时交易:考虑计算复杂度,避免高频场景使用 Hamming_ROC。
四大指标横向对比总览
场景1:趋势市场(单边上涨)
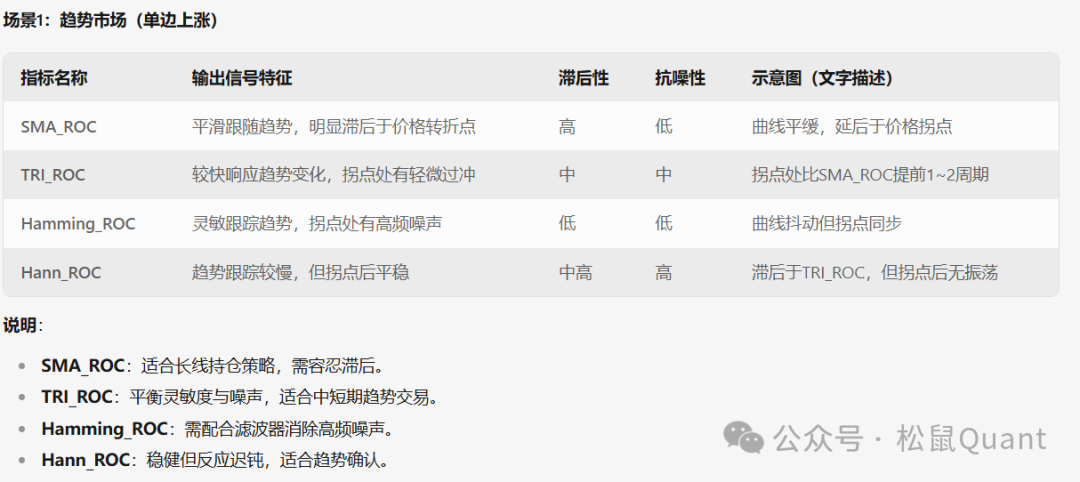
场景2:震荡市场(无明确方向)
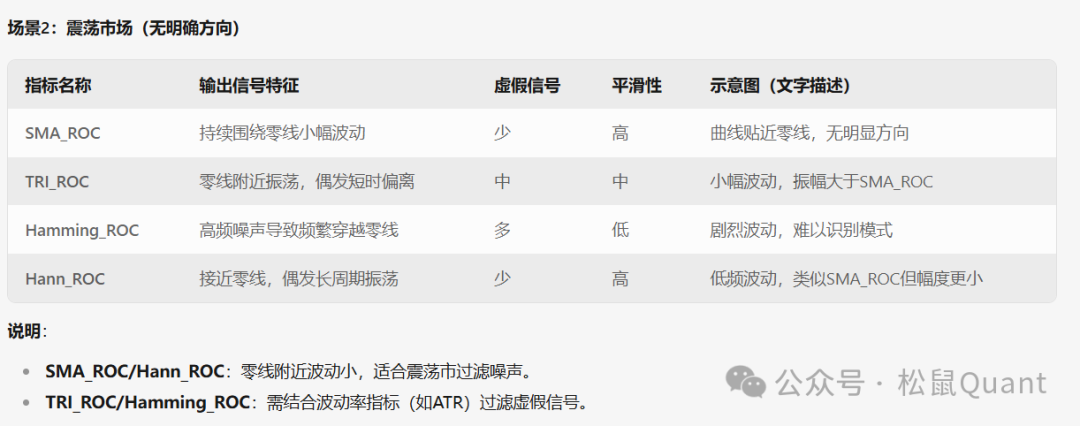
场景3:突发行情(价格跳空)

场景4:周期性信号(正弦波测试)
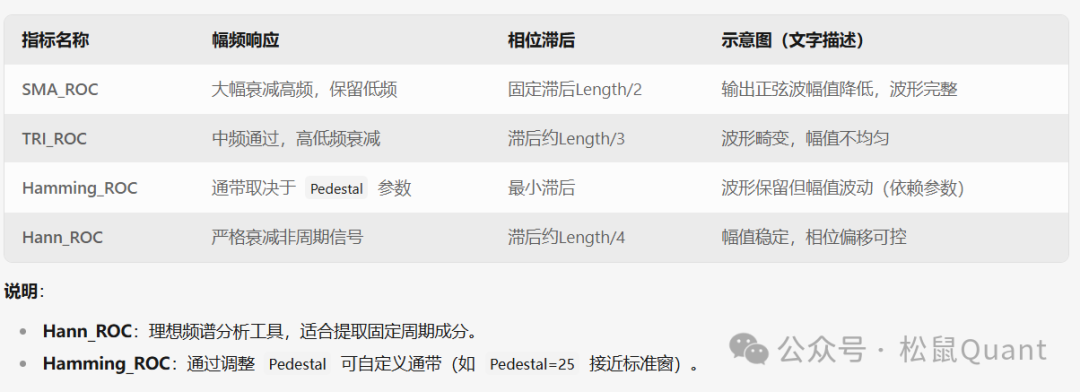
综合对比表
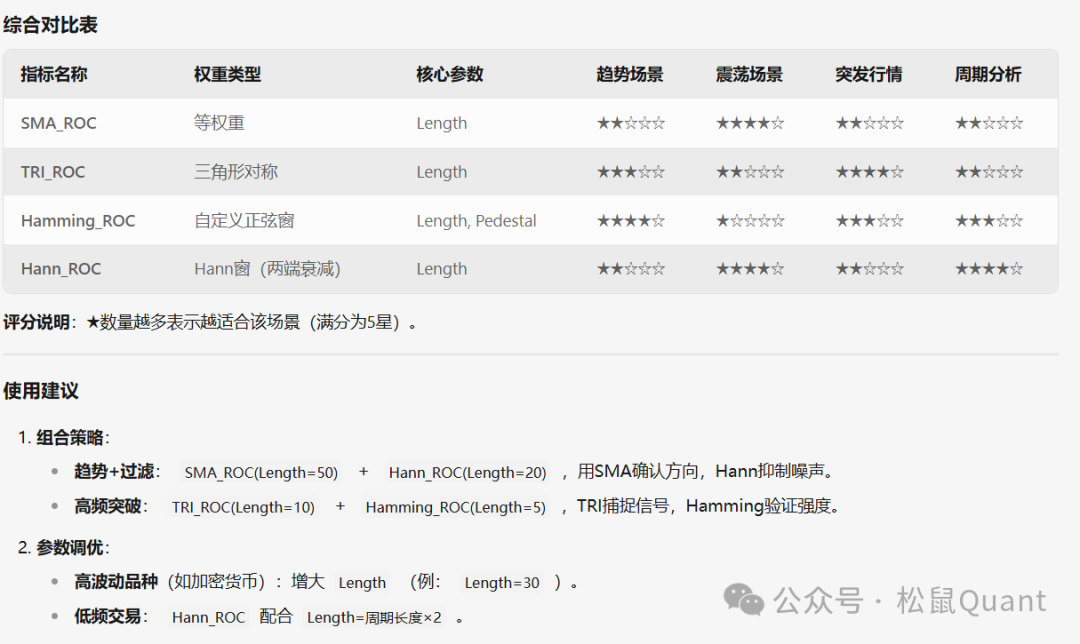
可视化模拟
震荡市场(价格→→→):SMA_ROC:--○--○--○--○--TRI_ROC:-○-○-○-○-○-○-Hamming_ROC:○○○○○○○○○○○○Hann_ROC:----○----○----
(注:▲表示信号拐点,○表示零线附近的微小波动)
如需具体参数回测或代码调试,可提供标的资产数据进一步分析。
源 码
VarsSeries<Numeric> Deriv; // 价格波导数序列,定义为当前K线的收盘价与开盘价之差(Close - Open)Series<Numeric> Filt; // 滤波器输出值,存储简单移动平均结果Series<Numeric> coef; // 累计系数(实际等于Length,但代码冗余保留)Series<Numeric> ROC; // 变化率(Rate of Change),用于衡量滤波器输出的变化速度Integercount; // 循环计数器,用于遍历历史数据
EventsOnBar(ArrayRef<Integer> indexs){// --- 1. 计算价格波导数 ---// 通过收盘价与开盘价的差值,捕捉当前K线的价格波动方向(正值为上涨,负值为下跌)Deriv = Close - Open;
// --- 2. 初始化滤波器及系数 ---Filt = 0; // 清空滤波器累加值 coef = 0; // 重置系数计数器(实际等同于Length)
// --- 3. 计算简单移动平均(SMA) ---// 循环累加过去Length个周期的Deriv值(等权重)forcount = 1 to Length {Filt = Filt + Deriv[count]; // 累加历史Deriv值(索引从1开始,对应前第count根K线) coef = coef + 1; // 实际等同于coef = Length }
// --- 4. 归一化滤波器输出 ---// 若系数非零(即Length>0),计算平均值If(coef <> 0) {Filt = Filt / coef; // 等效于 Filt = SMA(Deriv, Length) }
// --- 5. 计算变化率(ROC) ---// 通过当前滤波值与前一周期值的差分,乘以Length/(2π)缩放(近似角频率转换)ROC = (Length / 6.28) * (Filt - Filt[1]);
// --- 6. 绘制图表 ---PlotNumeric("Filt", Filt); // 输出滤波值PlotNumeric("ZeroLine", 0); // 绘制零线参考}
//------------------------------------------------------------------------// 编译版本 2025/03/17 163230// 版权所有 songshu123// 更改声明 TradeBlazer Software保留对TradeBlazer平台// 每一版本的TradeBlazer公式修改和重写的权利//------------------------------------------------------------------------
PS:2025俱乐部成员无需付费,请到网站后台下载即可。
2.TRI_ROC(三角形加权滤波 + 变化率)
.....................