使用 Python 机器学习预测黄金价格（完整源码）

松鼠Quant
2025-10-20


图片
量化策略开发，高质量社群，交易思路分享等相关内容

工具推荐

👉· 参数筛选工具

👉 ·Ai帮你编写策略

👉· 订单流图表

👉· 加入2025俱乐部

👉· Ai投研助手课程


『正文』

ˇ

让我们使用机器学习回归技术来预测最重要的贵金属之一黄金的价格。

我们将创建一个机器学习线性回归模型，该模型从过去的黄金 ETF (GLD) 价格中获取信息，并返回第二天的黄金价格预测。

步骤如下：

  • 导入库并读取黄金 ETF 数据

  • 定义解释变量

  • 定义因变量

  • 将数据拆分为训练数据集和测试数据集

  • 创建线性回归模型

  • 预测黄金ETF价格

  • 绘制累积收益

  • 如何使用这个模型来预测每日走势？


导入库并读取黄金 ETF 数据

首先要做的事情是：导入实施此策略所需的所有必要库。

1.png

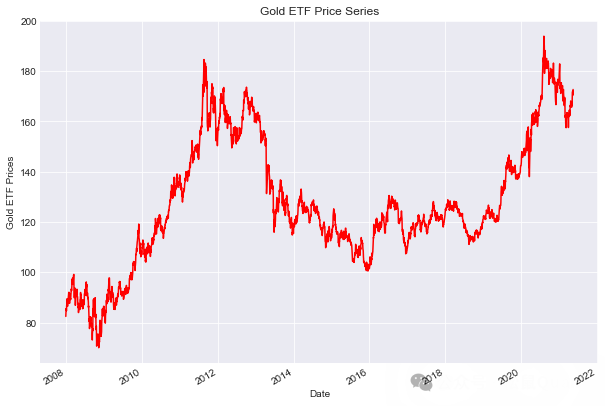
然后，我们读取过去 12 年的每日黄金 ETF 价格数据并将其存储在 Df 中。我们删除不相关的列，并使用 dropna() 函数删除 NaN 值。然后，我们绘制黄金 ETF 收盘价。

2.png

图片

定义解释变量

解释变量是被操纵以确定第二天黄金 ETF 价格价值的变量。简而言之，它们是我们想要用来预测黄金 ETF 价格的特征。

该策略的解释变量是过去3天和9天的移动平均线。我们使用 dropna() 函数删除 NaN 值并将特征变量存储在 X 中。

但是，您可以向 X 添加更多您认为有助于预测黄金 ETF 价格的变量。这些变量可以是技术指标、其他 ETF（例如黄金矿商 ETF (GDX) 或石油 ETF (USO)）的价格，或美国经济数据。

定义因变量

同样，因变量取决于解释变量的值。简而言之，这就是我们试图预测的黄金 ETF 价格。我们将黄金 ETF 价格存储在 y 中。

3.png将数据拆分为训练数据集和测试数据集

在此步骤中，我们将预测变量和输出数据拆分为训练数据和测试数据。训练数据用于通过将输入与预期输出配对来创建线性回归模型。

测试数据用于估计模型的训练情况。

  1. 前 80% 的数据用于训练，其余数据用于测试

  2. X_train 和 y_train 是训练数据集

  3. X_test 和 y_test 是测试数据集

  • 4.png

为了进一步分解，回归用自变量解释了因变量的变化。因变量 - 'y' 是您要预测的变量。自变量 -“x”是用于预测因变量的解释变量。以下回归方程描述了该关系：5.png

然后我们使用 fit 方法来拟合自变量和因变量（x 和 y），以生成回归系数和常数。

6.png

输出：线性回归模型

黄金 ETF 价格 (y) = 1.20 * 3 天移动平均线 (x1) + -0.21 * 9 天移动平均线 (x2) + 0.43（常数）

预测黄金ETF价格

现在，是时候检查模型是否在测试数据集中有效。我们使用训练数据集创建的线性模型来预测黄金 ETF 价格。预测方法查找给定解释变量 X 的黄金 ETF 价格 (y)。

7.png

图片

图片

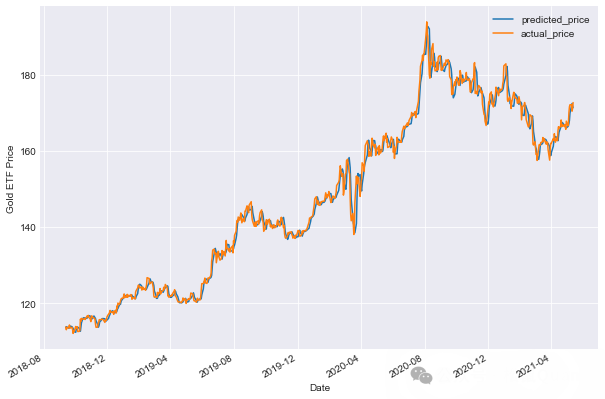
现在，让我们使用 Score() 函数计算拟合优度。

8.png

输出：99.21

可以看出，模型的 R 平方为 99.21%。R 平方始终在 0 到 100% 之间。接近 100% 的分数表明该模型很好地解释了黄金 ETF 的价格。

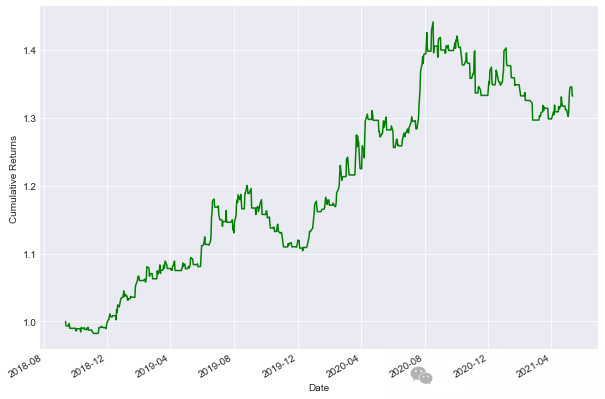
绘制累积收益

我们来计算该策略的累积收益来分析其表现。

  1. 计算累计收益的步骤如下：

  2. 生成黄金价格的每日百分比变化

  3. 当第二天的预测价格高于当天的预测价格时，创建以“1”表示的买入交易信号。否则不采取任何立场

  4. 通过将每日百分比变化与交易信号相乘来计算策略回报。

  5. 最后，我们将绘制累积收益图。

gold = pd.DataFrame()
gold['price'] = Df[t:]['Close']gold['predicted_price_next_day'] = predicted_pricegold['actual_price_next_day'] = y_testgold['gold_returns'] = gold['price'].pct_change().shift(-1)
gold['signal'] = np.where(gold.predicted_price_next_day.shift(1) < gold.predicted_price_next_day,1,0)
gold['strategy_returns'] = gold.signal * gold['gold_returns']((gold['strategy_returns']+1).cumprod()).plot(figsize=(10,7),color='g')plt.ylabel('Cumulative Returns')plt.show()

gold['strategy_returns'] = gold.signal * gold['gold_returns']((gold['strategy_returns']+1).cumprod()).plot(figsize=(10,7),color='g')plt.ylabel('Cumulative Returns')plt.show()

输出如下：

图片

我们还将计算夏普比率。


# Calculate sharpe ratio

sharpe = gold['strategy_returns'].mean()/gold['strategy_returns'].std()*(252**0.5)'Sharpe Ratio %.2f' % (sharpe)


输出如下：“夏普比率 1.06”

如何使用这个模型来预测每日走势？

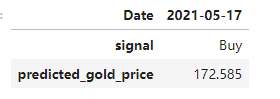
您可以使用以下代码来预测黄金价格，并给出是否应该买入 GLD 或不持仓的交易信号。

10.png

输出如下图：

图片

加小松鼠VX：viquant01

图片

发送：Gold   领取完整源码



分享